347
Table of Contents
For What Values Of M Does Graph Of Y = 3×2+7x+M Have 2X-Intercepts?
In this article, we explain the solution of “For What Values Of M Does The Graph Of Y = 3×2 + 7x + M Have Two X-Intercepts?”. First of all, we will talk about top websites which give so much information about every solution.
quora.com
For the x-intercept, put y=0.
the equation becomes, 3×2 +7x +m =0
Now find the discriminant, D=(49 – 4*3*m) >0 (For the roots should be distinct and accurate)
49>12m
or, m<49/12
Thus the value of m lies between (-infinity, 49/12 ).
protonstalk.com
The graph is a parabola with the most petite point. So, Substitute the smallest value in the equation y = 3x^2 + 7x + m. Thus the graph has two x-intercepts. The value at a minor point must be less than 0. The chart is a parabola with the smallest where x= -b/2a = -7/6.i.e
3(49/36) – 49/6 + m < 0
49/12 – 49/6 + m < 0
(49-98)/12 + m < 0
-49/12 + m < 0
m < 49/12
wyzant.com
The graph is a parabola with the smallest where x= -b/2a = -7/6. You should sketch it!
To have two x-intercepts, the value at a minor point must be less than 0, i.e.
3(49/36) – 49/6 + m < 0
49/12 – 49/6 + m < 0
(49-98)/12 + m < 0
-49/12 + m < 0
m < 49/12
cuemath.com
Question: For What Values Of M Does The Graph Of Y = 3×2 + 7x + M Have Two X-Intercepts?
Solution: The above equation is a polynomial that, when plotted, looks like a parabola. It is understood that the value of the variable “y” at the point of intersection with the x-axis is “zero” when the parabola crosses the x-axis. As a result, by changing the value of “y” in the following equation to zero, we get:
0 = 3×2 + 7x + m
To factorise the preceding quadratic equation, we must first determine the value of m. The remaining two components of the equation, 3×2 and 7x, may be used to calculate the probable value of “m.” As a result, the proper value of m is “2.” We may factorise the following equation by substituting the value of m.
0 = 3×2 + 7x + 2
0 = (x + 2)(3x + 1)
As no other value of m can factorise the above equation, m = 2 is a unique number. When the equation above is solved, we get two discounts of x when y = 0, x = -2 and x = -1/3. Hence, the equation will have two intercept values for m = 2.
What m values cause the graph of y = 3×2 + 7x + m to have two x-intercepts?
Summary:
The parabola contacts the x-axis twice at (-2, 0) and (-1/3, 0) for m = 2.
gauthmath.com
Question
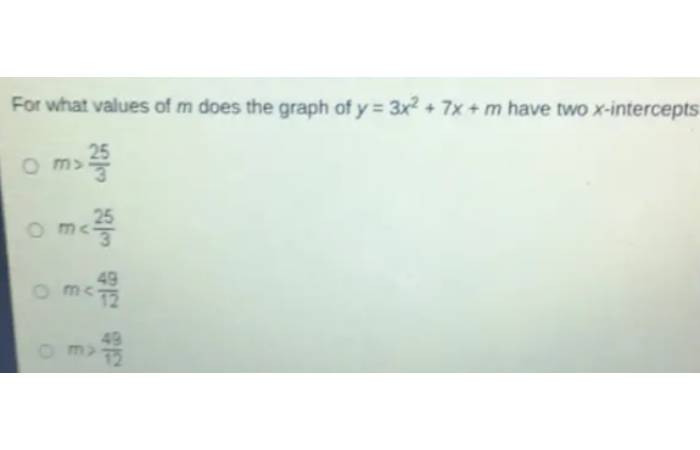
Answer
C
Explanation:
A
Depending on the number of possible solutions:
Rearrange the unknown terms to the left side of the equation as follows:
Lower the most common element that exists on both sides of the inequality:
Divide both sides of the inequality by the variable’s coefficient:
Rewrite this as a fraction:
Get the outcome:
False
True or false?
