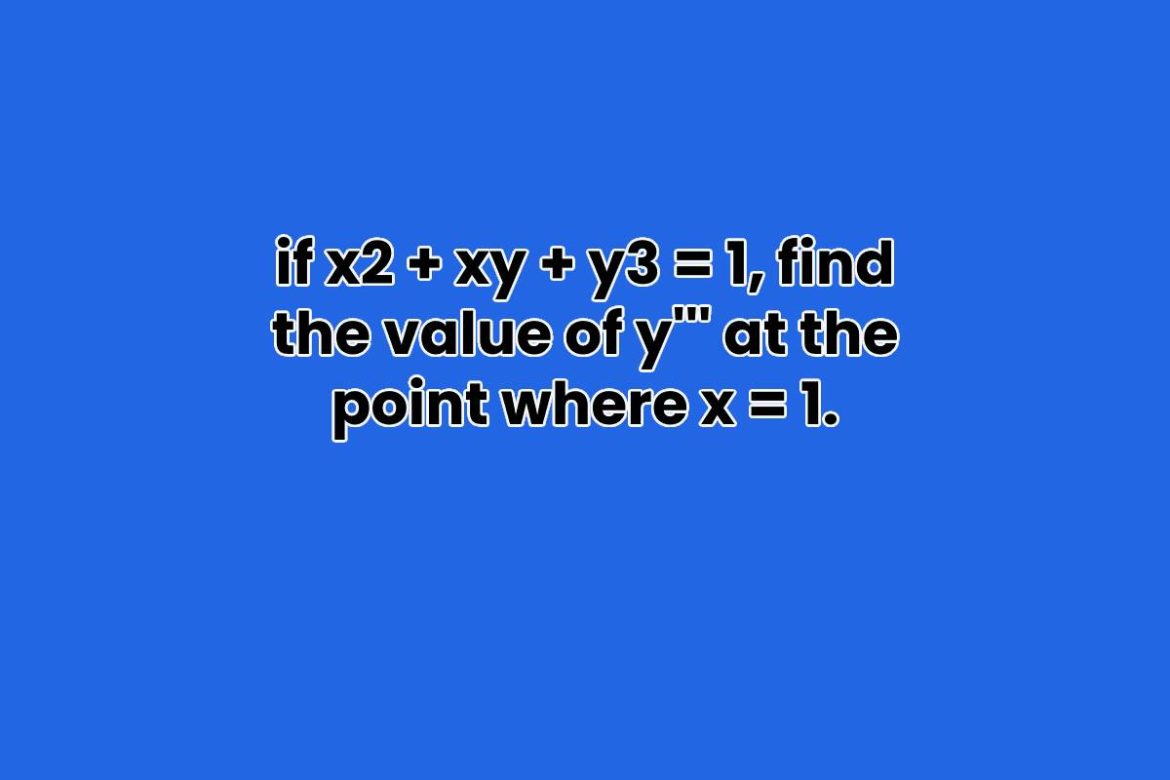- First of all, we want to talk about how to find the value of “if x2 + xy + y3 = 1, find the value of y”’ at the point where x = 1″. Here we have so many websites to give an excellent answer to this question. Like chegg.com/, math.stackexchange.com/, homework.study.com/ and also etc. All these websites are trying to provide perfect and also proper solutions for students.
Table of Contents
Question – if x2+xy+y3=1, find the value of y at the point where x =1
When I search for “if x2 + xy + y3 = 1, find the value of y”’ at the point where x = 1†I saw this below one,
They are not providing the exact answer for this “if x2 + xy + y3 = 1, find the value of y”’ at the point where x = 1″ question. No problem, we have so many other websites also. So next, we will look into math.stackexchange.com/. Let’s see what they are trying to say.
math.stackexchange.com
y′=−2y+3y2
Then trying to take the second derivative using the quotient rule.
- y′′=(y+3y2)(0)−(−2)(y+3y2)′(y+3y2)2
- (y+3y2)′=(1)(dydx)+6y(dydx)=−2y+3y2+−12yy+3y2=−2−12yy+3y2
- y′′=0−(−2)(−2−12yy+3y2)(y+3y2)2=−4+24yy+3y2(y+3y2)2=−4+24yy+3y2∗1(y+3y2)2
- y′′=4+24y(y+3y2)3
At this point, I’m not sure if this is right. But I went and tried for the third with a more quotient rule!
y′′′=(y+3y2)3(24)(dydx)−(4+24y)((y+3y2)3)′(y+3y2)6
Before I can finish that problem, I need the derivative of (y+3y2)3… for this, I need to use the chain Rule.
if f(x)=x3 then f′(x)=3x2 If we then let g(x)=y+3y2 then g′(x)=1+6y leaving us with…
3(y+3y2)2∗(1+6y)
Plugging that back into the rest of the problem, we get…
y′′′=(y+3y2)3(24)(dydx)−(4+24y)(3(y+3y2)2∗(1+6y))(dydx)(y+3y2)6
factoring out a (y+3y2)2, I get
y′′′=(y+3y2)2(y+3y2)(24)(dydx)−(4+24y)(3(1+6y))(dydx))(y+3y2)6
cancelling out for…
- y′′′=(y+3y2)(24)(dydx)−(4+24y)(3(1+6y))(dydx))(y+3y2)4
- y′′′=24y(1+3y)(dydx)−12(36y2+12y+1)(dydx)(y+3y2)4
- y′′′=−48y(1+3y)y+3y2+24(36y2+12y+1)y+3y2(y+3y2)4=−48y(1+3y)+24(36y2+12y+1)y+3y2(y+3y2)4
Then finally…
y′′′=−48y(1+3y)+24(36y2+12y+1)y+3y2∗1(y+3y2)4
y′′′=−48y(1+3y)+24(36y2+12y+1)(y+3y2)5
homework.study.com
According to homework.study.com, to solve the problem, “if x2 + xy + y3 = 1, find the value of y”’ at the point where x = 1″.
Question:
If x2+xy+y3=1, find the value of y′′′ at the point where x = 1. Use Implicit differentiation.
Implicit Differentiation and Quotient Rule – point where x

Any function f(w,s)=c is called an implicit function for that derivative of ′s′ w.r.t ′w′
is given by; s
dsdw=−(∂f∂w∂f∂s)
Let, function F(x)
in the form of fractions such that;
F(x)=p(x)q(x)
Derivative of F(x)
is given by;
dFdx=ddx(p(x)q(x))
dFdx=q(x)dpdx−p(x)dqdx(q(x))2
https://brainly.in – point where x
Given
x² + xy + y³ = 1
x = 1
To find
The value of y at the point where x = 1.
Solution
If x² + xy + y³ = 1
We can find the value of y at the point where x = 1 by substituting the value of x in the given equation.
So,
x² + xy + y³ = 1
Substitute x = 1,
1² + (1)y + y³ = 1
1 + y + y³ = 1
y + y³ = 1 – 1
0y + y³ = 0]
y ( 1 + y²) = 0
1 + y² = 0
y² = -1
y =
Final answer
The value of y at the point where x = 1 is
Answer
y = -1
4
Explanation
x2+xy+y3=1. (if x is 1)
1×2+1×y+y×3=1
2+y+3y=1. (put 2 to another side)
y+3y=1-2. add 3y and y,subtract1-2 )
4y=-1
y=-1 or y= (4)power -1
4