Table of Contents
mathway.com/ – Equation is Y = 9×2 + 9x – 1 Rewritten in Vertex Form
Algebra Examples
General Problems
Algebra
Find the Vertex Form y=9x^2+9x-1
y=9×2+9x−1
While the square for 9×2+9x−1
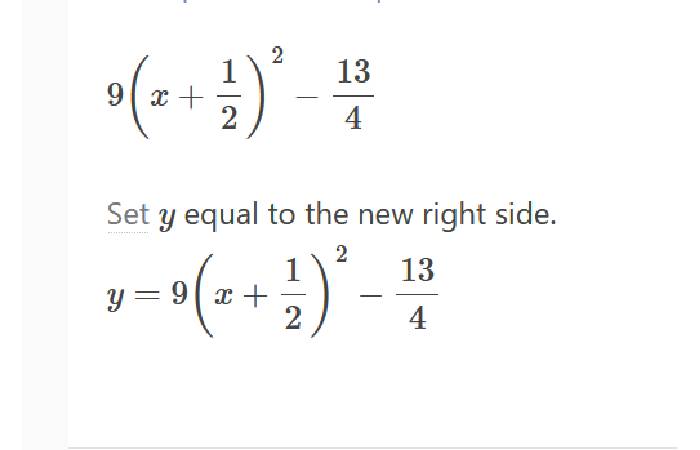
Which equation is y = 9x^2 + 9x – 1 rewritten in vertex form?

The equation is y = 9×2 + 9x – 1 rewritten in vertex form?
Recent Inquiries in Mathematics
Tony is employed in a lawn maintenance business. Therefore, wants to make at least 15% off to reward members from A shop. Tony trims ten lawns. For each yard he mows, he receives a $12 bonus in addition to his $9.25 hourly wage. What is the price break on the $215 worth of goods?
A circle has a surface area of 16 m2. In meters, what is the circumference? What is the value of x in the percentage below? Please explain your response in terms of that number. 10/30=x/15 A. 5 B. -5 C.20 D.50
Which equations depict circles whose centre is on the y-axis and whose diameter are 12 units? Pick two possibilities. x2 + (y – 3)2 = 36 x2 +
gauthmath.com/

Gauth Tutor Solution
Answer

Explanation

Similar Questions
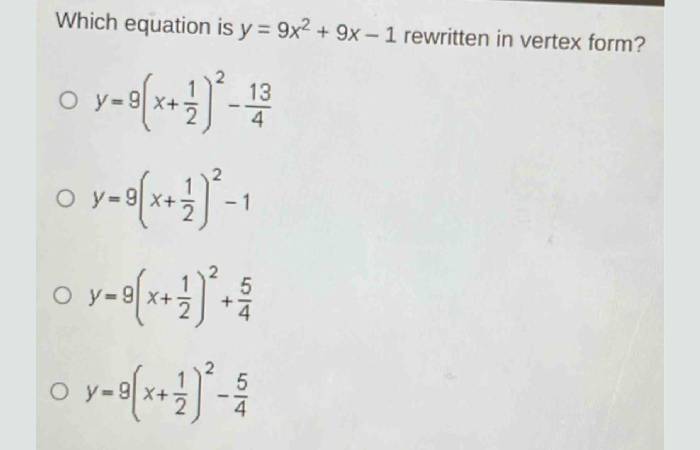


quizlet.com – Equation is Y = 9×2 + 9x – 1 Rewritten in Vertex Form?
In which equation is y=9×2+9x-1 rewritten in vertex form?
1)1) y=9y=9 (xx + half) squared minus fourteenths;
2)2) y=9y=9 (xx + 1/2) squared minus 1;1;
3)3) y=9y=9 (xx + one-half) squared + 5/4;
4)4) y=9y=9 (xx + half) squared minus five-fourths.
Step 1
Finding an equivalent expression, or one that has the same value as the supplied expression by rewriting it in vertex form, is necessary.
numerade.com/ – Equation is Y = 9×2 + 9x – 1 Rewrite in Vertex Form
In vertex form, whose equation is y = 9×2 + 9x – 1? 1) y = 9 (x + half) squared minus fourteenths 2) y = 9 (x + 1/2) squared minus 1 3) y = 9 (x + 1/2) squared plus five-fourths 4) y = 9 (x plus one-half) squared minus 5/4
geteducationskills.com/
What Is Vertex Form? Example
A vertex form is a location in geometry where two or more curves, lines, or edges intersect. As a result of this definition, vertices are the points where two lines intersect to make an angle, as well as the corners of polygons and polyhedra. A square, for example, has four corners, each of which is referred to as a vertex. Vertices is the plural version of vertex. The term vertex is most typically used to refer to a polygon’s corners.
An included angle is created when two lines intersect at a vertex. The internal angle of a polygon is the included angle at each vertex. This is not the term’s exact mathematical definition, vertex is also occasionally used to denote something’s “top” or high point, such as the vertex of an isosceles triangle, which is the “top” corner opposite its base.
Vertex Form of a Quadratic Equation
How do you graph quadratic equations in vertex form?
Explanation:
Quadratic Equations in Vertex Form have a normal form:
y=f(x)=a(x−h)2+k, where
(h,k) is the Vertex
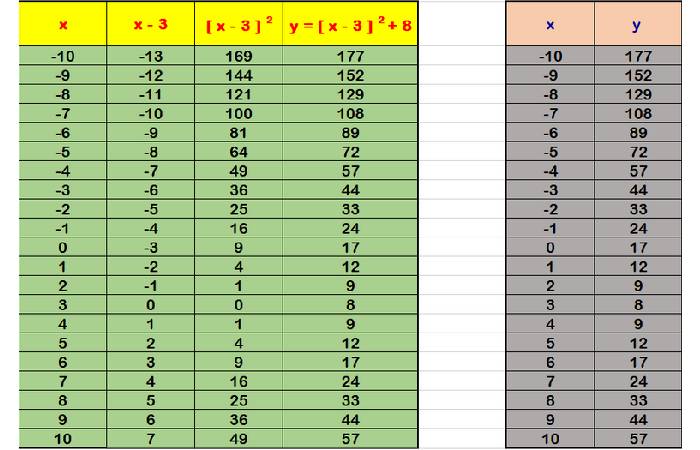
Let us assume a quadratic equation in Vertex Form:
y=f(x)=(x−3)2+8, where
a=1;h=3;k=8
Hence, Vertex =(3,8)
To find the y-intercept, set x=0
y=(0−3)2+8
y=9+8
y=17
Hence, the y-intercept: (0,17)
We can use a table of values to draw the graph: